What casinos hide. Part 2: Volatility
Understanding volatility: why a million spins might still not be enough
Last time we explored the odds of hitting a max win. Now let’s look at something casinos are even more reluctant to discuss: slot volatility.
The most common answer you’ll hear is:
“If volatility is low, you win often but small amounts; if it’s high, you win rarely but big.”
A perfect example of this is a screenshot from one of the most volatile and popular games out there — DOA2 (Dead or Alive 2).
Supposedly to make it easier for us, providers use vague adjectives instead of actual numbers: high, low, extreme, medium, and so on.
Why is this a problem?
First, you can’t even compare “high” to “high.” Two slots from the same provider might both say “high volatility,” yet differ by three or four times if you actually look at the numbers.
Second, these labels are basically useless.
It is like if every bank just said “low interest rate,” without ever telling you if that means 2% or 20%.
Just fluffy words with no actual figures. That is exactly what they want.
I see this as pure manipulation. I want to know exactly how often and how much, and I want to be able to compare real numbers, not vague adjectives.
The math behind it: standard deviation as the real measure of volatility
Fortunately, in some places we are finally seeing real numbers.
For example, on NoLimit’s site they actually list the standard deviation (σ). This is not just pretty marketing words, it is a concrete way to show the spread.
What do these numbers mean?
So what are you supposed to do with these figures? How can you tell if 18 is a lot or a little, and why does that get labeled as “extreme volatility”?
It does not even sound that extreme. Let’s break it down.
In classical probability, a standard deviation (σ) of 18 means that your result for a single trial typically fluctuates by about ±18 units around the expected value.
If your bet is $1, that would roughly translate to outcomes ranging from –$18.04 to +$17.96.
Of course in practice you cannot lose $18 on a single $1 spin. This is because a slot’s payout distribution is not actually normal. That is why it makes much more sense to analyze results over large distances, like tens of thousands of spins, rather than just looking at individual spins.
The Central Limit Theorem (CLT) guarantees that the final distribution will become roughly normal only with a very large number of spins. Besides, nobody walks into a casino to make just one spin.
A practical look: the DOA2 example
Let’s see what the expected results look like using DOA2. This slot has three different bonus rounds, each with its own volatility:
Train Heist — SD 9.2
Old Saloon — SD 18.8
High Noon Saloon — SD 45.1
The standard deviations and other slot parameters were calculated based on more than 100 million spins in the slot’s demo mode.
Here and throughout we will use ±3σ under the Central Limit Theorem to capture about 99.7% of all possible outcomes.
Expected results after 10,000 spins
Let’s see what kind of variance you can expect after 10,000 spins at $1 each.
Expected result by RTP: –$320
Expected range under the CLT (±3σ):
Train Heist: from –$3,080 to +$2,440
Old Saloon: from –$5,960 to +$5,320
High Noon Saloon: from –$13,850 to +$13,210
Even with a standard deviation of 9.2 (Train Heist), the range is huge. Instead of the expected –$320 you could easily end up at –$3,000.
For High Noon Saloon with a standard deviation of 45.1, it is even more striking. The potential loss can actually exceed your entire deposit. This happens because for such high volatility 10,000 spins is still nowhere near enough. It takes a much larger number of spins before the Central Limit Theorem truly kicks in.
Results after 100,000 spins
Expected result by RTP: –$3,200
Expected range under the CLT (±3σ):
Train Heist: from –$11,928 to +$5,528
Old Saloon: from –$21,035 to +$14,635
High Noon Saloon: from –$45,986 to +$39,586
Even after 100,000 spins, there is still a chance to end up in profit with Train Heist. For High Noon Saloon, the spread is still enormous, exceeding almost half of the entire turnover of bets.
Results after 1,000,000 spins
Expected result by RTP: –$32,000
Expected range under the CLT (±3σ):
Train Heist: from –$59,600 to –$4,400
Old Saloon: from –$88,400 to +$24,400
High Noon Saloon: from –$167,300 to +$103,300
It sounds almost unbelievable, but even after a million spins you could still end up $103,000 ahead, or take a loss that is $135,000 worse than expected.
Comparing it to roulette
To really understand how volatile this is, let’s compare these standard deviation values to betting on a single number in European roulette, which has just 37 pockets (including zero).
For a straight-up bet on a single number, the standard deviation is about 5.8 when wagering $1 per spin.
When I was grinding my first bonus 10 years ago, I thought betting on a single number in roulette was the ultimate risk. But that does not even come close to many slots.
Now imagine a roulette wheel like this:
Train Heist (SD 9.2) is equivalent to betting on a number in roulette with 86 pockets.
Old Saloon (SD 18.8) is like betting on a number in roulette with 354 pockets.
High Noon Saloon (SD 45.1) is the same as betting on a number in roulette with a staggering 2,034 pockets.
It is a rough comparison, but it really puts into perspective just how massive the risks are when you play slots with different levels of volatility.
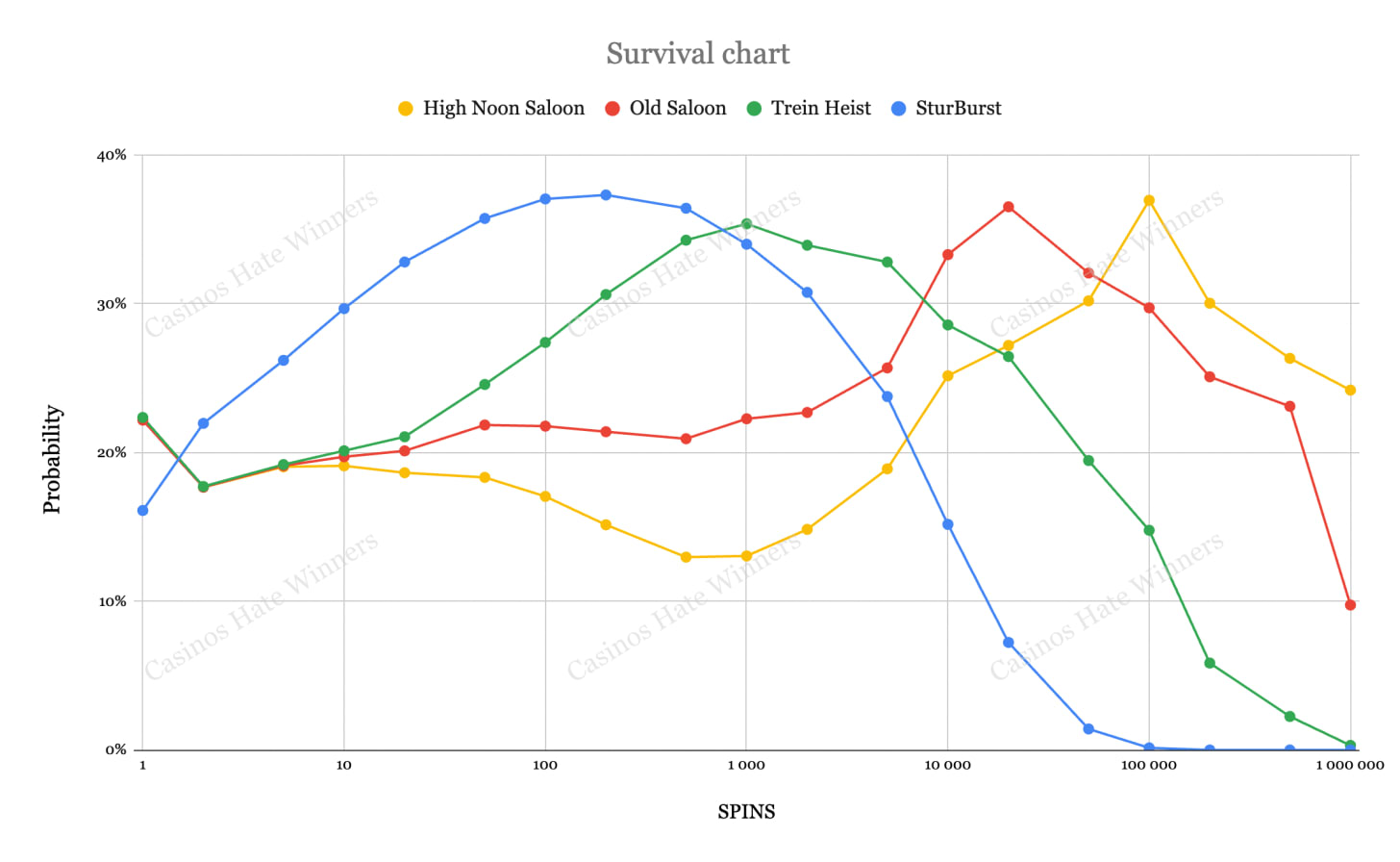
Survival chart
To better understand distance and volatility, let’s look at this survival chart. It shows the probability of ending up in profit after a certain number of spins.
For context, I added the low-volatility slot StarBurst (SD 4.3) for comparison.
Key takeaways:
After 100,000 spins, the chance of finishing in profit with StarBurst drops close to zero. Its best odds are about 37%, which happens after just 200 spins.
Train Heist does not reach zero probability until nearly a million spins.
Even after 1,000,000 spins, High Noon Saloon still has about a 25% chance to end in profit, with its optimal zone around 100,000 spins, right where StarBurst’s odds have already collapsed.
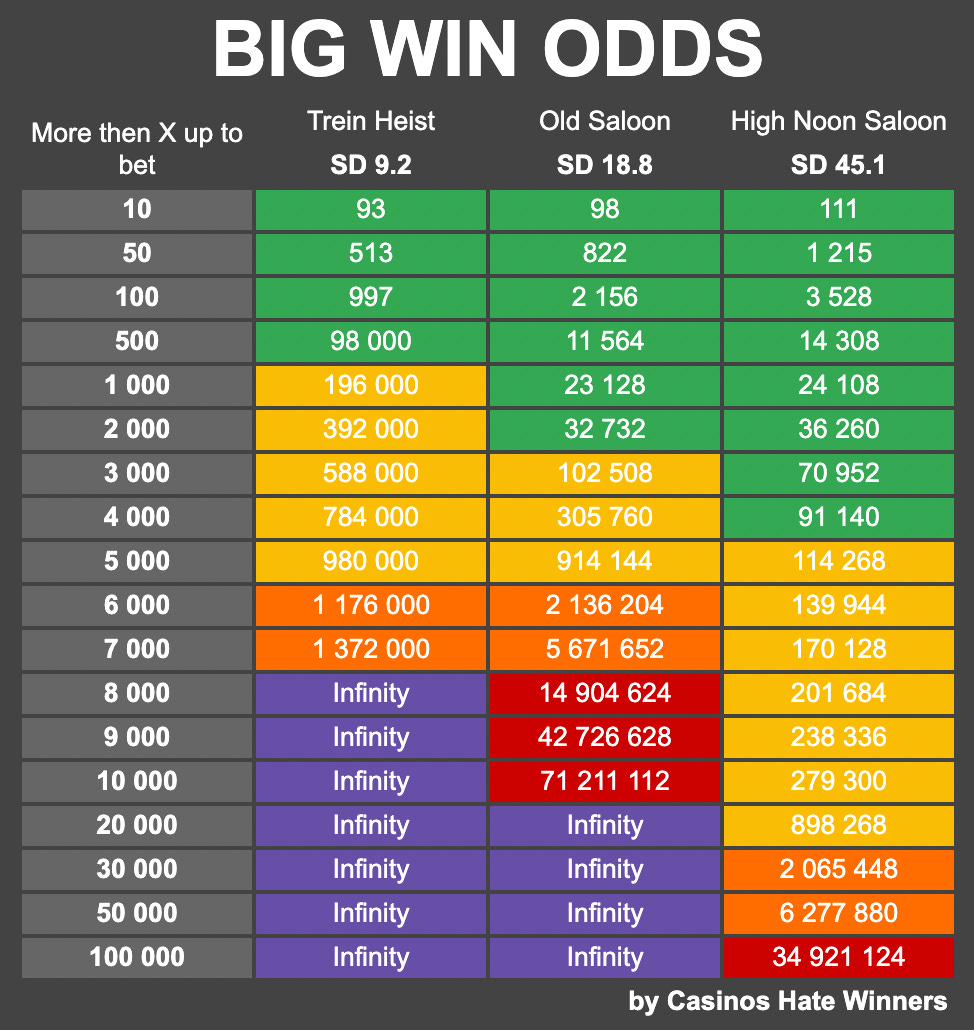
How volatility impacts the odds of big wins
Now let’s take a closer look at how volatility affects different sizes of wins.
Smaller multipliers like x50 show up far more often in low-volatility slots:
In Train Heist (SD 9.2), a x50 win happens about once every 500 spins.
In High Noon Saloon (SD 45.1), it is roughly once every 1,200 spins.
Bigger wins, like x5,000 and above, mostly appear in high-volatility slots:
For High Noon Saloon, a x5,000 hit comes up roughly once every 114,000 spins.
For Train Heist and Old Saloon, it is closer to once in a million.
Massive wins like x15,000, x50,000, or x100,000 only ever show up in High Noon Saloon. In Train Heist and Old Saloon, these payouts never appeared even after running 180 million spins.
Key takeaways
The main points to remember:
Volatility is not just “often or rarely.”
It is a precise measure of how wide your results can swing, best shown as a number like standard deviation (SD).
Distance is critical.
Even with volatility around 9, the spread over 100,000 spins can be huge.
For extremely volatile slots, even a million spins might not be enough for RTP to stabilize.
The survival chart shows where your best chances to end up ahead are.
For slots like StarBurst, the peak is already within a few hundred spins.
For High Noon Saloon, it only comes around 100,000 spins, and even after a million there is still a chance to be ahead.
Feel free to ask anything. And let me know in the comments what volatility means to you and how you see it. Would love to hear your take on it.